15 — JULIA Types

Tuesday, 25 February 2020 Julia Belyakova

This time, we will talk about:

• multiple dispatch and why it is cool; Things we learned about nominal and structural subtyping in 14 — More Types will come in handy.

• how it is supported in the Julia language;

• how types interact with the dispatch mechanism.

The Extensibility (aka Expression) Problem

Consider the following task.

Write an interpreter for this simple language of arithmetic:

Expr ::= int | - Expr | Expr + Expr

Any expression in this language evaluates to an integer.

Take a moment to think about the task. How would you solve it in your favorite language? What data types and functions/methods would you define?

Now, consider another task.

Extend the language of arithmetic expressions to support integer equality check and conditional:

Expr ::= ... | Expr == Expr | if Expr Expr Expr

In the extended language, an expression evaluates to either an integer or a boolean. The equality check is defined only for integers, and the if-expression takes a boolean condition.

Write a type checker and an interpreter for this language.

If you were allowed to reuse/extend code written for the first task, what would be your solution to the new task? What data types would you have to add and/or modify? What functions/methods would you have to add and/or modify?

Most likely, your solution falls into one of the two categories:

• Functional style

  1. Original language

     Datatype for expressions with three variants, e.g.

     data Expr = EInt(Int) | ENeg(Expr) | EAdd(Expr, Expr)

     +

     Datatype for integer value

     +

     Function for interpreter, e.g.

     interpreter :: Expr -> Value

     interpreter(expr) =

     case expr of

     EInt(v) -> ...

     ...

  2. Extended language

     Modified datatype for expressions, e.g.

     data Expr = ... | EEq(Expr, Expr) | EIf(Expr, Expr, Expr)

     +

     Modified datatype for values

     +

     Datatype for types

     +

     Function for type checker

     +

     Modified function for interpreter, e.g.

     interpreter :: Expr -> Value

     interpreter(expr) =

     case expr of

     ...

     EEq(eleft, eright) -> ...

     EIf(econd, ethen, eelse) -> ...

• Object-oriented style

  1. Original language

     Class hierarchy for values

     +

     Class hierarchy for expressions with a method for interpreter in each class, e.g.

     abstract class Expr {

     abstract Value interpret();

     }

     class EInt extends Expr {

     Int val;

     ...

     Value interpret() { ... }

     }

     class ENeg extends Expr {

     Expr left;

     Expr right;

     ...

     Value interpret() { ... }

     }

     class EAdd extends Expr { ... }

  2. Extended language

     Class hierarchy for types

     +

     Modified classes with a new method for type checker

     +

     Concrete classes for new expressions with methods for type checker and interpreter, e.g.

     class EEq extends Expr {

     Expr left;

     Expr right;

     ...

     Type check() { ... }

     Value interpret() { ... }

     }

     class EIf extends Expr { ... }

Look through the both bullet points above and notice which parts of the code have to be modified.

Which of the approaches above (functional or object-oriented) works better for extending data? And which one is better for adding functionality?

The intuition "works better" can be expressed as "does not require modifying existing code".

• With the functional approach, we don’t need to modify any code to add a type checker, so it works better for adding functionality.

• With the object-oriented approach, we don’t need to modify any code to add new expressions, so it works better for extending data.

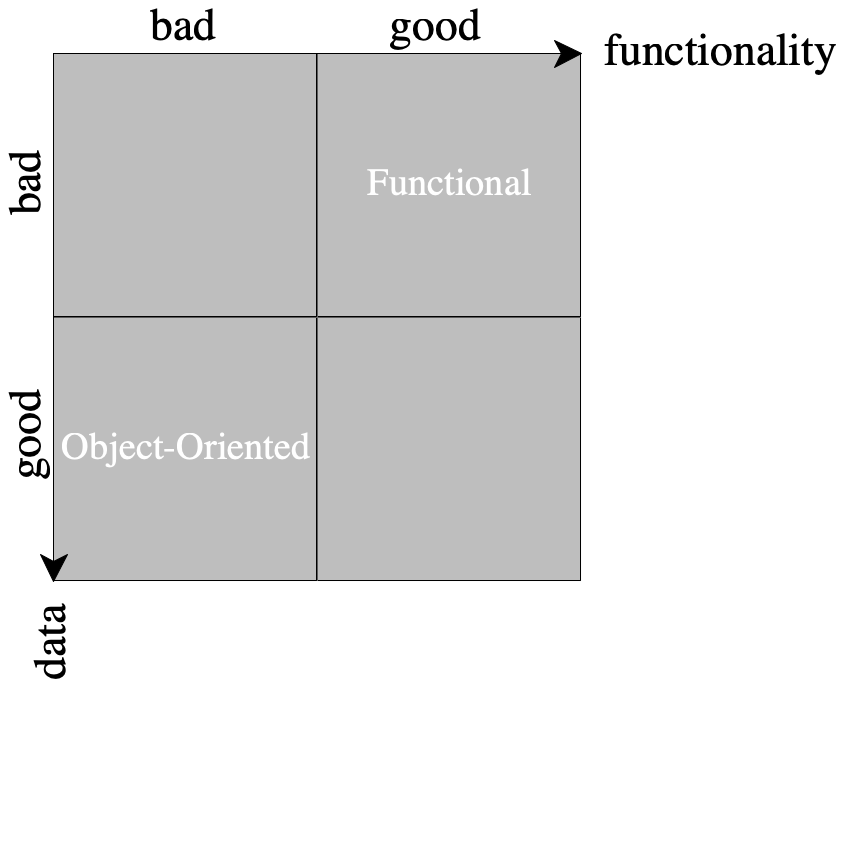
This challenge of extending data and adding functions over the data without modifying existing code is known as the extensibility problem (aka expression problem).

Visually, it is usually represented with a diagram, where "Good" means "easy to extend without modifying existing code". See figure 67 for the basic diagram.

Figure 67: The Basic Extensibility Problem

In most languages, without planning for extensibility from the start, one would not be able to get both these dimensions (as you have just experienced yourself). There are workarounds and design patterns, e.g. extensible visitors, tagless final, object algebras, but they would normally be injected after revising the code, once the need for extensions has become clear. (Note that a good old visitor pattern simply reverses the problem for an object-oriented language.)

Figure 68: The Extensibility Problem, Solved With Patterns

In a language with multiple dispatch, however, the extensibility problem is solved trivially! The word “trivial” refers to just one dimension, the “control” aspect of the problem. The other dimension concerns static typing, which we do not address here. Without planning and thinking ahead, one is able to both extend data and add functionality without touching any existing code. Thus, if we limit the diagram only to pure language mechanisms, multiple dispatch takes the sweet spot; see figure 69.

Figure 69: The Extensibility Problem, Solved Linguistically

Logical vs Physical Types (again)

Question. What is the fundamental difference between an abstract class/interface and a "normal" class?

Normal classes give rise to objects, whereas abstract ones don’t.

Remember we talked about logical and physical types in 11 — Types & Proofs?

• Logical types are used by the type checker; they enable reasoning about programs without running the programs.

• Physical types are used by the interpreter/compiler; they are needed for running the programs.

Let’s look at Java from this logical/physical types prospective. Are non-abstract classes logical or physical? Why? What about abstract classes and interfaces?

• All classes and interfaces induce logical types that can be used by the type checker.

• In addition, non-abstract classes (but not interfaces) give rise to run-time objects, so they also act as physical types.

We can summarize this reasoning in a diagram (from now on, "interface" stands for both interfaces and abstract classes, and "class" stands for non-abstract classes):

A type checker does not care about the physical side of classes. An interpreter does not care about the logical side of classes, but it needs to know something about interfaces for dynamic dispatch.

Note that in our toy language with structural types (from lectures and home assignments), logical types were completely decoupled from run-time values. In the presence of classes, however, this is not the case any more. Every class serves as both logical and physical type because it gives rise to two things:

• type annotation used by the type checker statically;

• type tag used by the interpreter at run-time (every object is "tagged" with the class name it has been created with).

Loosely speaking, the instanceof operation checks whether a type tag adheres to a type annotation.

Ignoring the implementation details of dynamic dispatch, let us revise the diagram:

Simple Interpreter in JULIA

Let’s get back to the very first task and write an interpreter for the simple language of arithmetic:

This time, we will write it in Julia, a language with multiple dispatch. Note that Julia is not statically typed.

As usual, we start with a data representation for expressions.

abstract type ExprAST end

struct EInt <: ExprAST

val :: Int

end

struct ENeg <: ExprAST

expr :: ExprAST

end

struct EAdd <: ExprAST

left  :: ExprAST

right :: ExprAST

end

What do you think is the difference between an abstract type and a struct? Just like interfaces, abstract types such as ExprAST do not give rise to data but make up nominal hierarchies. Structs such as EInt (called concrete types in Julia), on the other hand, are data constructors that produce values "tagged" with the struct name, just like non-abstract classes produce objects.

Note that <: in Julia is really nothing but subtyping. Neither abstract types nor structs can have methods inside; abstract types are just names, and concrete types cannot be further subtyped, so there is nothing to inherit/extend. Despite its name, struct is a nominal type. (If you are wondering why concrete types cannot be subtyped, the answer is — for the sake of performance.)

Ok, we have the data definition. Let’s write an interpreter! What should it return? In our simple language, the result of evaluating an expression is an integer:

IValue = Int

Can the interpreter ever error? Why? Let’s write some examples/unit tests:

iBig = 4543534543

eInt1   = EInt(1)

eIntBig = EInt(iBig)

eNegIntBig = ENeg(eIntBig)

eAddN3Neg5 = EAdd(EInt(-3), ENeg(EInt(5))) ;# -3 + (-(5))

@test interpret(eInt1) == 1

@test interpret(eIntBig) == iBig

@test interpret(eNegIntBig) == -iBig

@test interpret(eAddN3Neg5) == -8

Since no run-time errors are possible, the interpreter implementation is trivial:

;# ExprAST -> IValue

interpret(expr::EInt) = expr.val

interpret(expr::ENeg) = - interpret(expr.expr)

interpret(expr::EAdd) = interpret(expr.left) + interpret(expr.right)

interpret(s::String) = s

The set of all methods with the same name is called a generic function (not to confuse with generics and polymorphic functions). At run-time, every function call such as interpret(ENeg(EInt(4))) is dispatched to the best method available (we’ll talk about this mechanism soon).

Ok, our interpreter seems to work. But what if we forgot to define a method for ENeg? In the interpret(ENeg(EInt(4))) case, we would get a run-time error, of course!

The role of type annotations

Let’s forget about the interpreter for a second. Consider the following program (pseudo code):

Can you translate it to Java and Julia? What happens when we run the programs in each case?

Thanks to the type checker, the dec("hell") call will never be evaluated.

Whenever a call to dec is being evaluated, we can be certain that inside dec, variable x contains an integer value.

Because Julia is not statically typed, no static type error is reported for dec("hell"), so the call will be evaluated. Then, because all function calls are handled by dispatch and there is no dec method for a String argument, this call will fail at run-time. Note that we will not evaluate the body of dec(::Int)!

Whenever a call is being dispatched to the dec(::Int) method, we can be certain that inside dec(::Int), variable x contains an integer value.

Thus, Julia does not use type annotation as logical types for type checking, but the interpreter does rely on them at run-time.

Note. Type annotations are not required in Julia. We can write methods such as

f(x) = x + 1

and then inside f, variable x can contain any value. A method without type annotations is equivalent to a method for ::Any, where Any is a supertype of all types (often referred to as "top").

Subtyping Dispatch

How does the run-time system know which method to dispatch to? Clearly, in the current interpreter example, there is just one method that can handle ENeg:

;# ExprAST -> IValue

interpret(expr::EInt) = expr.val

interpret(expr::ENeg) = - interpret(expr.expr)

interpret(expr::EAdd) = interpret(expr.left) + interpret(expr.right)

interpret(ENeg(EInt(4))) ;# -4

How about the following definitions?

;# ExprAST -> String

toString(expr::ExprAST) = "ExprAST"

toString(expr::EInt) = "$(expr.val)"

toString(expr::ENeg) = "-($(toString(expr.expr)))"

toString(ENeg(EInt(4))) ;# "-(4)"

Intuitively, there are two methods applicable to an ENeg value, toString(::ExprAST) and toString(::ENeg). And we would like the dispatch mechanism to pick the latter one, because it is more specific. But what does it mean to be applicable and more specific?

Formally, the intuition translates to the use of subtyping. Dynamic dispatch of toString(ENeg(...)) is resolved in two steps:

1. Find all toString methods applicable to ENeg tag. For this, check subtyping between the type tag and type annotation of every toString method:

   • ENeg <: ExprAST ? Yes, toString(::ExprAST) is applicable.

   • ENeg <: EInt ? No, toString(::EInt) is not applicable.

   • ENeg <: ENeg ? Yes, toString(::ENeg) is applicable.

2. Select the most specific method out of the applicable ones. For this, check subtyping between type annotations of the methods.

   • ENeg <: ExprAST ? Yes, toString(::ENeg) is more specific than toString(::ExprAST).

Thus, we have two applicable methods and one of them is more specific than the other, so the call is dispatched to the more specific one.

In the interpreter example, the set of applicable methods is a singleton set, so there is no choice but to pick interpret(::ENeg). If we remove this method, the set becomes empty and we get the "no method" error.

Do you think other errors are possible? What about step 2? Is it always possible to find the best method?

Multiple (Symmetric) Dispatch

Wait a minute! Didn’t we promise to talk about multiple dispatch? So far, all the methods accept one argument, and we can easily write similar code in Java using classes and dynamic dispatch.

Very well, let’s define equality for expressions in the Expr language. How do we do this in Julia? Any guesses? The solution should not be surprising (the last method catches situations where the arguments have different tags, in which case they are definitely not equal).

==(e1::EInt, e2::EInt) = e1.val == e2.val

==(e1::ENeg, e2::ENeg) = e1.expr == e2.expr

==(e1::EAdd, e2::EAdd) = e1.left == e2.left && e1.right == e2.right

==(e1::ExprAST, e2::ExprAST) = false

And what about Java? Because here, dynamic dispatch works only for one argument, we have to inspect the tag of the second argument manually, for example:

In Julia, multiple dispatch does all the tag-inspection work for us.

Note. Dispatch in Julia is called symmetric because all the arguments are treated as equally important. Can you think of a different approach? It is called an asymmetric multiple dispatch. In this case, we process arguments left to right, and filter applicable methods based on the type of current argument.

The truth about multiple dispatch

There is nothing special about multiple symmetric dispatch. It is just a single dispatch on tuple types!

• Every method in Julia takes one argument, but the argument is a tuple.

• A tuple is a generalization of a pair; it represents one or more values bundled together, e.g. ("hey", true, 3).

So, in addition to nominal types such as ExprAST and EInt, Julia supports several structural types such as tuples. Subtyping of tuple types is rather straightforward (tuples are often denoted as s × t):

What else can go wrong with dispatch

Consider the following methods, assuming that Nat <: Int and Int(v) converts a Nat to an Int.

add(x::Int, y::Nat) = add_int(x, Int(y))

add(x::Nat, y::Int) = add_int(Int(x), y)

Is there anything weird about these definitions? What happens when we call add with two natural numbers? Let’s walk through the method resolution process:

1. Find applicable methods.

   • (Nat, Nat) <: (Int, Nat) ? Yes, add(::Int, ::Nat) is applicable.

   • (Nat, Nat) <: (Nat, Int) ? Yes, add(::Nat, ::Int) is applicable.

2. Find the best method.

   • (Int, Nat) <: (Nat, Int) ? No, add(::Int, ::Nat) is no more specific than add(::Nat, ::Int).

   • (Nat, Int) <: (Int, Nat) ? No, add(::Nat, ::Int) is no more specific than add(::Int, ::Nat).

Neither of the applicable methods is the most specific! In this case, we get an "ambiguity" error:

Note. With an asymmetric dispatch, the ambiguity error is impossible. Why is that?

JULIA Solution to The Extensibility Problem

Finally, we are ready to solve the extensibility problem! Let’s add the support for the extended language:

First of all, we need to extend the data definition:

struct EEq <: ExprAST

left  :: ExprAST

right :: ExprAST

end

struct EIf <: ExprAST

econd :: ExprAST

ethen :: ExprAST

eelse :: ExprAST

end

In the extended language, the result of interpretation can be either integer or boolean:

IValue = Union{Int, Bool}

To avoid interpreting bad expressions and producing run-time errors, we need a type checker. Of course, we have to define types first:

abstract type Ty end

struct TInt  <: Ty end

struct TBool <: Ty end

;# instances for convenience

const tInt  = TInt()

const tBool = TBool()

And type errors:

;# Custom exception for type checker

struct TypecheckException <: Exception

msg :: String

end

const ERRTyIntDomain  = "domain error: integer expected"

const ERRTyIfCond     = "boolean expected for if condition"

const ERRTyIfBranches = "same type expected for if branches"

errorType(msg) = throw(TypecheckException(msg))

Finally, the type checker:

;# ExprAST -> Ty|Error

;# Type checks [expr] and either returns its type or throws a type error

typecheck(expr::EInt) = tInt

typecheck(expr::ENeg) = typecheckMatch(expr.expr, tInt, ERRTyIntDomain)

typecheck(expr::EAdd) = let

typecheckMatch(ExprAST[expr.left, expr.right], tInt, ERRTyIntDomain)

tInt

end

typecheck(expr::EEq) = let

typecheckMatch(ExprAST[expr.left, expr.right], tInt, ERRTyIntDomain)

tBool

end

typecheck(expr::EIf) = let

typecheckMatch(expr.econd, tBool, ERRTyIfCond)

(tthen, telse) = (typecheck(expr.ethen), typecheck(expr.eelse))

tthen == telse ? tthen : errorType(ERRTyIfBranches)

end

;# (ExprAST, Ty) -> Ty|Error

;# Type checks [expr] and matches its type with [ty]

typecheckMatch(expr::ExprAST, ty::Ty, errMsg) =

typecheck(expr) == ty ? ty : errorType(errMsg)

;# (ExprASTList, Ty) -> TyList|Error

;# Type checks expressions in [exprs] list and matches their types with [ty]

typecheckMatch(exprs::ExprASTList, ty::Ty, errMsg) =

map(expr -> typecheckMatch(expr, ty, errMsg), exprs)

Assuming we will run the interpreter on well-typed expressions, the extension to the interpreter is rather modest:

interpret(expr::EEq) =

interpret(expr.left) == interpret(expr.right)

interpret(expr::EIf) =

interpret(interpret(expr.econd) ? expr.ethen : expr.eelse)

Note that we did not have to touch any old code to extend the language! We simply defined new data and added new methods. Recall figure 69, the diagrammatic placement of multiple dispatch with respect to the extensibility problem. Of course, nothing comes for free. Because multiple dispatch is so flexible, someone or something has to suffer.

• It can be hard for the user to predict which methods are called here and there.

• Dispatch is not easy to implement efficiently. Julia is JIT-compiled and employs type inference to "statically" resolve as many function calls as possible.

• Fully-fledged multiple dispatch might be hard to type check, depending on the the kind of logical types and guarantees one wants to provide.