►Principles of Programming Languages
▼Lectures
•21 — State Machines
7.7.0.3
    ← prev  up  next → 

21 — State Machines

Tuesday, 24 March 2020

Presenters (1) Mike Sarfaty & Liam Weldon, (2) Corrine Cella & Liam Douglass

If we applied the continuation-passing transformation to our interpreter, we would obtain a state machine. This approach is “design via program transformation” and is definitely something you should keep in mind.

We will skip this derivation step but still study this state machine. Today’s lecture is preparation.

State Machines

Depending on when/from whom you took Fundamentals I, some of this material may have been covered. The relevant sections are the very basics of finite-state machines and a domain-specific language for finite-state machines.

You have encountered many state machines in your life: light switches, traffic lights, soda machines, and so on.

A traffic light can be in about three major states: red, yellow, and green (plus blinking yellow or red plus turned off). It transitions from red to green, from green to yellow, and from yellow to read. These transitions are triggered by the passage of time.

A soda machine also comes with two states. In the first state it is ready to accept your selection. When you select a “classic foobar,” it transitions to the second state—waiting for your money. The transition back to the first state takes place when you have paid the required sum or canceled the transaction (which may happen because too much time passed).

Every state machine comes with states—which is where the name comes from—and transitions from states to states. These transitions can be triggered by various things: an input, the passage of time, the state of the machine itself, and so on. If the number of possible states is finite—like for traffic lights or soda machines—we speak of a finite state machine; otherwise we just say state machine.

Specifying State Machines

Based on the informal description, the essence of a state machine is

  • the set of states a machine can be in;

  • transitions that take a machine from one state to another;

  • the state(s) in which a machine starts—called initial state(s)

  • the state(s) in which a machine shuts down—called final state(s)

By showing red, a traffic light causes traffic to stop and thus prevents potential accidents. It is therefore called a fail-safe state. When machines misfunction they also tend to be engineered to go into a fail-safe state. The soda machine, for example, goes into a “waiting for your selection” state when turned on. A well-designed traffic light will go into a “red” state.

image

Figure 78: A finite-state machines as a diagram

A “lexer” is the piece of a language parser that recognizes and differentiates individual words. Remember that in this course we leave this task to your JSON library.

A lexer is also a finite state machine. Its states are “have seen this sequence of letters”, starting in a state where no letters have been recognized. It ends when an expected word has been seen. So a “machine” for recognizing the word "raise" from Python’s syntax can be characterized like this:

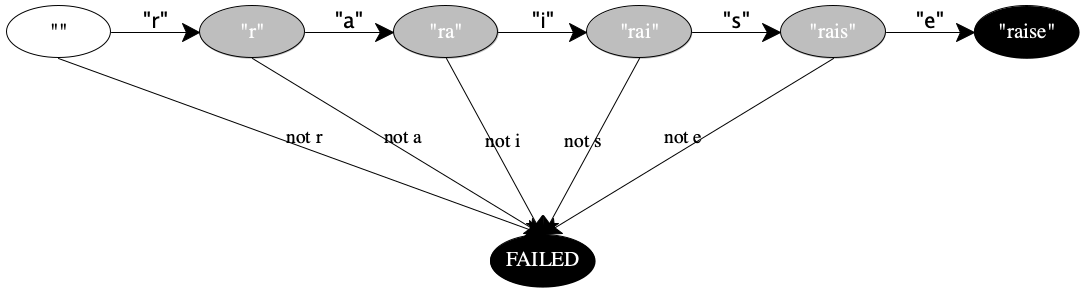
  • states "" (no letter seen), "r" (just “r”), "ra", "rai", "rais", "raise" and FAILED;

  • transitions when the letter "r" shows up and the machine is in state "", it transitions to "r"; for any other letter, it moves to FAILED

    Stop! Figure out the remaining transitions

  • the only initial state is "";

  • the two final states are "raise" (signaling success) and FAILED (signaling failure).

The above is a typical description and, usually, works reasonably well.

In addition to the above, people also use two other means to specify state machines: diagrams and tables.

Figure 78 shows how to turn this natural-language description into a diagram with a relatively obvious interpretation. The white node is an initial state, the black ones are final states, and the gray ones are intermediate states. The labels on the arrows specify when the lexer transitions from one state to another. Although every intermediate state connects to two successor states, the machine is deterministic because the transition labels are mutually exclusive.

Here is a table representation of the same finite machine:

current state

     

transition

     

next state

""

     

r

     

"r"

"r"

     

a

     

"ra"

"ra"

     

i

     

"rai"

"rai"

     

s

     

"rais"

"rais"

     

e

     

"raise"

While the set of initial and final states are left implicit, it is easy to infer them from such a table. Because "" never shows up in the right column and "raise" never in the left one, the two are the initial and final states, respectively. The FAILED state is left implicit in such tables; it is assumed to exist because the machine must also transition somewhere when it is in the first state and the letter a shows up.

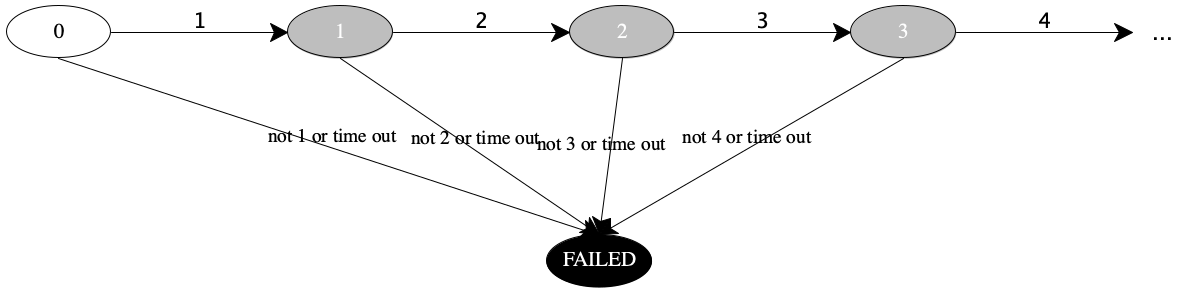
image

Figure 79: An infinite-state machine as a diagrams

State machines do not have to come with a finite set of states or even a finite number of reasons for transition from one state to another. Let’s look at a toy example:

  • states all natural numbers

  • transitions when the machine is in state n and its “input” within a certain time interval is n + 1, it transitions to state n + 1; otherwise it goes to a FAILED state.

  • 0 is the initial state

  • FAILED is a final state

Yes, this machine cannot succeed, which is why we call it “toy.”

Figure 79 shows how such a machine might be specified as a diagram. The dots at the end of the top are suggestive and perhaps not good enough for someone who wishes to implement the machine. The following is a literal translation of the diagram into a table format:

current state

     

transition

     

next state

0

     

1

     

1

1

     

2

     

2

2

     

3

     

3

3

     

4

     

4

...

     

...

     

...

As before, the FAILED state is left implicit. Here is a truly concise tabular specification:

current state

     

transition

     

next state

     

n

     

n + 1

     

n + 1

     

for all n ∈ N

n

     

k

     

FAILED

     

for k ≠ n + 1

And it is also complete.

The Stepper as a State Machine

The Stepper you know from Fundamentals I is also a state machine. For simplicity, let’s look at a stepper for just the arithmetic expressions in a programming language. Here is a grammar of ArithmeticExpr
  e = n
  | (e o e)
     
  o = +
  | -
  | *
  | /
Here n n1 and n2 stand for arbitrary numbers.

We use fully parenthesized expressions to avoid precedence, which is not essential to the current topic.

To specify the stepper, we introduce an additional notion, namely the idea of an evaluation context. Informally speaking, an evaluation context is an arithmetic expression with one hole in place of a sub-expression. The hole is precisely where the next computation must take place. For example,

((1 + 2) * (3 - [---]))

is such an evaluation context where [---] is the hole. As before, we assume that evaluation proceeds from right to left. Filling an evaluation context means placing an expression into its hole, which produces a complete expression. If E stands for the above evaluation context, E [42] means E with 42 put into its hole. Similarly, E [(84 / 21)] means putting (84 / 21) into the hole of E, which yields

((1 + 2) * (3 - (84 / 21)))

The data definition (grammar) for these contexts can be derived from the grammar for arithmetic expressions:
  E = [---]
  | (ae + E)
  | (E + n)
  | (ae - E)
  | (E - n)
  | (ae * E)
  | (E * n)
  | (ae / E)
  | (E / n)
First, the grammar must include the hole. Second, a literal number cannot contain a hole, so we ignore it. Third, every proper expression gives rise to two kinds of context: when the right sub-expression is already evaluated to a number and when it is not. This yields nine production clauses in total.

Now we can use evaluation contexts to describe how the machine proceeds with a concise table:

current

     

next

     

if

E [(n1 + n2)]

     

E [n]

     

n = n1 + n2

E [(n1 - n2)]

     

E [n]

     

n = n1 - n2

E [(n1 * n2)]

     

E [n]

     

n = n1 * n2

E [(n1 / n2)]

     

E [n]

     

n = n1 / n2

When we write something like E [(n1 + n2)], we mean a pattern where n1 and n2 can be any number.

The table implies the following four-clause description:

  • states all ArithmeticExprs are states

  • transitions determining the result in the rightmost un-evaluated sub-expression is the only kind of transition though there are four flavors

  • every arithmetic expression is an initial state

  • all plain numbers are final states

Stop! Explain these four clauses based on the table.

Let’s work through the example of ((1 + 2) * (3 - (84 / 21))):

state

  

E

  

inside of E

((1 + 2) * (3 - (84 / 21)))

  

((1 + 2) * (3 - [---]))

  

(84 / 21)

((1 + 2) * (3 - 4))

  

((1 + 2) * [---])

  

(3 - 4)

((1 + 2) * -1)

  

([---] * -1)

  

(1 + 2)

(3 * -1)

  

[---]

  

(3 * -1)

-3

  

final state

The left column is the sequence of states that the machine assumes. The second and third column show how the machine partitions its state into an evaluation context E and an expression whose two sub-expressions are numbers. It uses these pieces to determine the next state of the machine.

Implementing State Machines

If a state machine reacts to notions other than its current state, the driver function must consume this input and manage it.

From a high-level perspective, a state machine like the stepper is a relatively simple program:
State driver(State initial_state) {
  State current = initial_state;
  while !(final_state_huh(current)) {
     current = transition(current);
     displayln(current);
  }
  // current is now a __final state__
  return current;
}
 
State transition(State current) {
   ...
  return next;
}
 
Boolean final_state_huh(State s) {
  ...
  return what_is_it;
}
It consumes an initial state and uses a transition function to compute the next. If desired, it can now display the transition and continue until the state is a final one.

Figure 80 displays the complete code for the ArithmeticExpr stepper. Its entry point is the driver function, which refers to the final? and transition functions. The first one is just number? here, the second one follows exactly the informal description.

Lectures/21/stepper.rkt

  #lang racket
   
  (require "while.rkt" "show-state.rkt")
   
  #; {ArithmeticExpr -> Number}
  ;; print each step of the calculation that reduces `expr` to a number
  (define (driver initial)
    (display "   ") (displayln initial)
    (define current initial)
    (while (not (final? current)) do
      (set! current (transition current))
      (show-state current))
    current)
   
  #; {ArithmeticExpr -> ArithmeticExpr}
  (define (transition ae0)
    (let --> ([ae ae0] [E HOLE])
    (match ae
      [(list (? number? n_1) '+ (? number? n_2)) (fill E (+ n_1 n_2))]
      [(list (? number? n_1) '- (? number? n_2)) (fill E (- n_1 n_2))]
      [(list (? number? n_1) '* (? number? n_2)) (fill E (* n_1 n_2))]
      [(list (? number? n_1) '/ (? number? n_2)) (fill E (/ n_1 n_2))]
      [(list ae_1 o (? number? n)) (--> ae_1 (fill E `[,HOLE ,o ,n]))]
      [(list ae_1 o ae_2)          (--> ae_2 (fill E `[,ae_1 ,o ,HOLE]))])))
   
  #; {E ArithemticExpr -> ArithemticExpr}
  (define (fill E inside)
    (match E
      [(? (curry equal? HOLE))   inside]
      [(list E o (? number? n)) (list (fill E inside) o n)]
      [(list ae_1 o E)          (list ae_1 o (fill E inside))]))
   
  #; {ArithmeticExpr -> Boolean}
  (define final? number?)
   
  (define HOLE '[---])
   
  ;; - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 
  (module+ test
    (require rackunit)
    (check-equal? (driver '((1 + 2) * (3 - (84 / 21)))) -3))
   

Figure 80: Implementing the Stepper State Machine

The transition function partitions the given expression into an evaluation context E and an ArithmeticExpr that has just two numbers as sub-expressions. It evaluates this inside expression and fills E with the resulting number. It is the driver function’s responsibility to continue until there is nothing left to do.

    ← prev  up  next →