►Principles of Programming Languages
▼Lectures
•20 — Control from CPS
7.7.0.3
    ← prev  up  next → 

20 — Control from CPS

Friday, 20 March 2020

Presenters (1) Mike Sarfaty & Liam Weldon, (2) Jack Mastrangelo, Jack Loar

Why CPS

Imagine you get a job, your job requires the production of JavaScript or TypeScript, and one day the team has the crazy idea that you should be able to interrupt a (perhaps long-running) event handler. For example, your JavaScript code may implement a simple IDE within the browser for kids to learn how to code.

Which is of course why I put big-bang into Fundamentals I way back in 2005. So how does JavaScript in the browser really work? How does big-bang work? It turns out this is the same question.

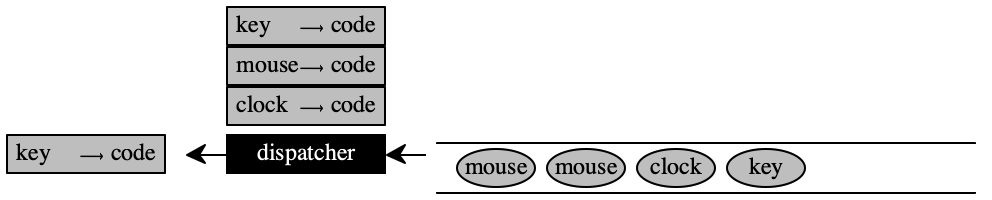
Your JavaScript program registers event handlers (possibly via frameworks such as Angular.JS, React.js, or Vue.js) with the JavaScript engine. From this perspective, the engine consists of two pieces: a queue into which events get deposited (by the OS component of the browser) and the dispatcher, which takes the first item in the queue and runs the appropriate piece of code.

the empty queue and dispatcher

image

a "key" event arrived, possibly with payload

image

the dispatcher reacts and runs the registered "key" handler

image

more events arrive, they all go into the queue until the current handler is finished

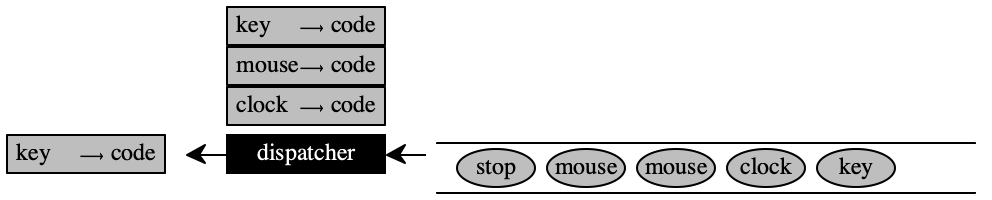
image

Figure 72: Event Handling a la JavaScript or big-bang

Figure 72 provides a graphical overview of the various stages in which a JavaScript programs runs within the browser. There are other kinds of events, and the details of how an event’s payload (the data representation of an event’s attributes) get to the respective handler, but these details are irrelevant. What is relevant is that once the dispatcher gives control to a handler, say the key handler in the figure, this handler code runs until it is finished. So if the key handler, for example, invokes the evaluator of an in-browser IDE,

how can we get to execute a "stop" event that is possibly implemented via a button in the browser?

(See WeScheme for an example; pursue the "coding" option and note the Stop button.)

This is where continuations and continuation-passing come to the rescue.

Halt

The simplest non-local control construct. On occasion a program’s computation reaches such a disastrous state that it must stop the execution, regardless of what else it should have computed.

A Java program may call System.exit in such situations. In Python, the language where everything is done “one way,” you have quit, exit, sys.exit, and os._exit; choose wisely. For Racket and the teaching languages we recommend error to signal an error; the racket/control library also offers abort, a request to stop the program immediately.

When a program is written in continuation=passing style, it is straightforward to implement a stop instruction: a function may simply not use its continuation.

   

expression

   

the continuation-passing version

Model PL

   

[call
  [fun f
    [node +
          [call f 1]
          42]]
  [fun x {stop x}]]

   

[call
  [call
    [fun k
      [fun f
        [call [call f
                    [fun ir
                      [call k
                            (node + ir 42)]]]
              1]]]
   [fun x x]]
 [fun k
   [fun x
    ; just don't use k
     x]]]

   

   

Racket

   

[[lambda (f)
   [+ [f 1] 42]]
 ; Racket has a real ‘stop‘
 [lambda (x)
   {abort x}]]

   

([(lambda (k)
   (lambda (f)
     ((f (lambda (ir)
            (k (+ ir 42)))) 1)))
 identity]
 (lambda (k)
   (lambda (x)
     ; just don't use k
     x)))

Catch and Throw

Exception handling is another form of non-local control that exists in every one of the programming languages you have chosen for this class. The idea dates back to the early days of Lisp, which in the late 1960s provided ERR and ERRSET. By 1972, it provided the catch-and-throw facility that we study here. For certain reasons, the invention was recently attributed to the CLU programming language in the late 1970s. For example, in Java you may use try, throw, and catch to attempt a computation, raise an exception if it fails, and pursue an alternative direction in response; JavaScript supports the same mechanisms. Python again supports a plethora of facilities: raise, try, except, else, and finally. In Racket we use with-handlers and raise for the same idea. Okay, Rust is different.

To keep things simple, we analyze a simple catch and throw facility here in terms of continuations passing:

  • [catch AssExpr] evaluates its sub-expression. If it yields an ordinary value, that is the result of the entire expression. If the evaluation of the sub-expression throws a value, it is the result.

  • [throw AssExpr] evaluates its sub-expression and “throws” its value to the catch expression in whose temporal extent it is currently evaluating—if any. If none, a throw terminates a program turning the value of its sub-expression into the result of the program.

Extending the grammar is the easy part:
(struct catch [bdy] #:transparent)
(struct throw [bdy] #:transparent)
 
; type CExpr extends AssExpr with
; – [catch CExpr]
; – [throw CExpr]
And here is a series of simple examples that illustrate the general explanation of how the two work:

evaluating the program

   

yields

   

remarks

[throw 42]

   

42

   

there is no catch to stop the throw

   

   

[node +
  [catch
    [throw 42]]
  1]

   

43

   

the catch stops the throw and evaluates the node expression

   

   

[node +
  [catch
    [throw 42]]
  [catch 1]]

   

43

   

the catch on the right plays no role; it is evaluated when the interpreter gets to throw

   

   

Remember “channels of communication” from 16 — Gradual Types? This is an example why we need to protect those.

[call [catch
        [call
          [call [fun one [fun two one]]
            [catch [throw 42]]]
          [throw [fun x x]]]]
      21]

   

21

   

the inner catch plays no role, because the interpreter never gets to it; indeed, it throws the wrong kind of value so that’s a “good thing”

[call [catch [throw [fun x x]]]
      [node + [catch [throw 20]] 1]]

   

21

   

each throw returns to its closest catch

The general explanation, as illustrated by the examples, suggest the following:

  • at any point during program evaluation, the cps transformation must designate a “throw” continuation;

  • throw uses this continuation as the designated continuation, calling it with the result of its sub-expression instead of the one that represents its control context;

  • catch changes this designated continuation while its body is evaluated and changes it back once the evaluation produces or throws a value.

We assume the Java convention here that identifiers starting with a dollar sign cannot be used by programmers; they are only acceptable in the context of abstract syntax trees.

Small changes to the cps function accomplish these three bullets, without touching the interpreter:

  • the cps function initializes a global variable named "$escape" that contains the current “throw” continuation:
    (define (cps expr)
      [decl "$escape" [fun final-result final-result] (receive-k expr)])

  • the transformation of throw in split-expr ignores the given k and instead dereferences "$escape":
    (define (split-expr ae k)
      (match ae
        ...
        [(throw bdy)
         (call (receive-k bdy) "$escape")] ...))

  • the transformation of catch in split-expr turns the given k into the new value for "$escape" and evaluates the expression’s bdy in the context of this continuation:
    (define (split-expr ae k)
      (match ae
        [(catch bdy)
         [call [fun "current"
                    [sequ (set "$escape" (make-escaper "current" k))
                          (call [receive-k bdy] "$escape")]]
               "$escape"]] ...))
    The function application [fun current ...] allows us to capture the current value of "$escape" because decl may not have variables on the right-hand side of declarations.

This leaves us with just the helper function for catch:
; {Var Var -> CExpr}
(define (make-escaper current k)
  [fun of-catch-escape
       [sequ
         [set "$escape" current]
         [call k of-catch-escape]]])
The function produces a continuation whose job it is to consume the value of the catch or some nested throw expression. The function proceeds in two steps. First it sets "$escape" to current, the variable that contains the old throw continuation. Second it calls the continuation of the catch expression on the given value.

Stop! What ensures that when catch is evaluated—in a regular manner or via a throw—that "$escape" refers to throw continuation that was in place when evaluation started?

Sadly many programmers and even language researchers without proper training often use the word “scope” instead—leading to many misunderstandings.

The evaluation of catch distinctly delimits a temporal interval with different ways of reaching the end. The modern terminology for such an interval is (dynamic) extent.

Stopify

So how do we solve the JavaScript problem?

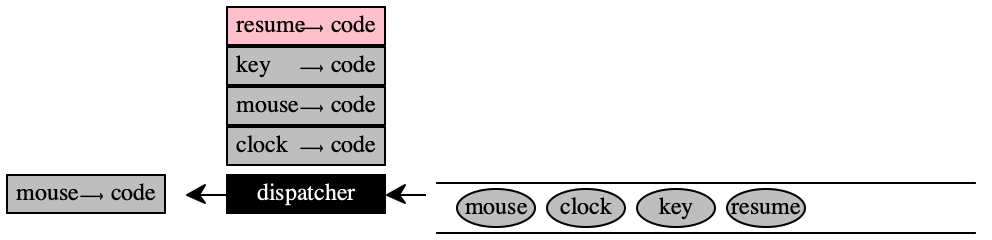
Roughly speaking, you could pipe your source code through a cps function for JavaScript and insert a communication to the dispatcher together with each call to a continuation. If the communication suggests a "stop" event must be handled, the dispatcher can register the current continuation a "resume this continuation" handler, insert a "resume" event into the queue, and move on to the next event.

The Stopify framework realizes just this idea automatically and is already in use at several companies. It is the result of relatively recent research (published at one of PL’s flagship conferences) and you are able to understand this work.

a "stop" event arrives and gets put up front because it is a priority queue

image

the event handler swaps the current handler’s continuation for the next event

image

Figure 73: Handling Stop

CPS Frees Us From the Meta-Language

We once again turn to the dual nature of programming languages—as mathematical ideas and physical artifacts (bits on a machine)—-to explain continuation-passing style transform of a program and the original as well as to the interpreter.

The first theorem states that we could use either an interpreter that evaluates function applications (including node) from right to left or left to right, and the result will stay the same.

Theorem interpreterRL{[call (cps p) [fun x x]]} == interpreterLR{[call (cps p) [fun x x]]} for any program p

Stated as a slogan, cps hands the power of flow of control to the source program.

CPS is correct

The second theorem tells us that the continuation-passing transform is correct.

Theorem interpreter{p} == interpreter{[call (cps p) [fun x x]]} for any program p

In particular, when p produces an integer, (cps p) when applied to the “stop” continuation—which just returns what it is given—produces the same integer. If the final value is a cell or function, the results are still the same but the theorem makes a less interesting statement than in the case of integers.

Theorems such as the one above reassure us at the mathematical level but also have “computational content.” That is, we can formulate them as property test cases, which can then be subjected to random testing. Figure 74 shows how we can turn the mathematical statement into a property, a function from AssExpr to boolean. Property testing—aka quickcheck testing—generates inputs for theorem and applies theorem many times to randomly selected AssExprs. The unit tests below show how this theorem works for some fixed cases.

Lectures/20/cps-theorem.rkt

  #lang racket
   
  (require "cps-theorem-imports.rkt") 
  ;; - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
  #; {AssExpr -> Boolean}
  (define (theorem program #:expected [expected #false])
    (equal?
     (or expected (interpret program))
     (interpret [call (cps program) [fun r r]])))
   
  ;; - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
  ;; "PROOF"
  (module+ test
    (require rackunit)
   
    (check-true (theorem [node + 1 1]))
    (check-true (theorem (call (fun x [node + x (node * x 2)]) 10)))
    (check-true (theorem (call (fun x [if-0 x 43 (node * x 2)]) 10)))
    (check-true (theorem (call (fun x [sequ [set x [node + x 1]] x]) 42)))
   
    (check-true (theorem
                 (decl g (fun x (node * x 10))
                       (decl f
                             (fun y
                                  (if-0 y
                                        1
                                        (call g (call f (node + y -1)))))
                             (call f 3))))))
   
  (provide theorem)
   

Figure 74: The Continuation-Passing-Style Correctness Theorem, Illustrated

Predictive Value and Debugging CPS

The second theorem is also a bit of a design guideline for manually and gradually applying the continuation-passing transformation to a program, possibly in your favorite programming language.

Let’s give the identity continuation a name in the Racket world:

(define halt-k (lambda (final-result) final-result))

The argument is called final-result because that’s what it is supposed to be. With this name in place, the theorem says “apply the cpsed programs to halt-k and it will produce the same result as the original.”

Now take a look at figure 75. It shows an attempt to introduce the continuation-passing style gradually for a program translated from our model language into Racket. Run the example. It will give the same result three times, suggesting that we converted the program properly.

Lectures/20/cps-example.rkt

  #lang racket
   
  (require "cps-theorem-imports.rkt")
   
  (define halt-k (λ (final-result) final-result))
   
  ;; - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
  ;; in our model language
   
  [call [fun f (node * (call f 10) (call f 20))]
        [fun x (node + x 42)]]
   
  ;; - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
  ;; in RACKET (or your favorite language) 
   
  ((λ (f) (* (f 10) (f 20)))
   (λ (x) (+ x 42)))
   
  ;; - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
  ;; equip first function with continuation for delivering result
   
  ((λ (f k) (k (* (f 10) (f 20))))
   (λ (x) (+ x 42))
   halt-k)
   
  ;; - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
  ;; equip second function for delivering a result, call it with halt-k
   
  ((λ (f k) (k (* (f 10 halt-k) (f 20 halt-k))))
   (λ (x k) (k (+ x 42)))
   halt-k)
   

Figure 75: A Gradual CPS Conversion

This is where a slightly stronger version helps a lot: Design Guideline

(interpreter p) == (interpreter [call (cps p) [fun x (raise x)]])

(Replace with throw, stop, raise in your favorite language.)

If we do this, we see that evaluating the third Racket expression yields a totally different answer.

Tail Positions and Tail Calls The reason is that halt-k is not called in a special position, namely, a place where there is nothing left to do.

The place within a function “where is nothing left to do” has a name: tail position (with respect to a function). Let’s investigate our entire model language for tail positions within a function [fun x ...]:

  • a plain number such as 42 is in tail position.

  • a plain variable, say x or y, is in tail position.

  • an (if-0 TST THN ELS) contains three sub-expressions: TST, THN, and ELS. The TST sub-expression is guaranteed not to be in tail position because after it is evaluated one of the other two expressions—THN or ELS—must be evaluated before the function may return a result.

    By contrast, the expression THN is in tail position and so is ELS.

  • a primitive operation of the shape (node o L R) contains two sub-expressions: L and R. Both must be evaluated and after their results become known more is to be computed. In the case of R, we must also compute the result of L. And in the case of L, we must still compute the o of the two values.

  • a function such as (fun y ...) is in tail position because, like a number, it is a value.

  • a function call of the shape (call F A) is like a primitive operation. Both F and A must be evaluated and after that the value of F must be called on the value of A.

  • a (set x R) expression must evaluate R and then perform a mutation on x.

  • a sequ expressions also contains two sub-expressions. After evaluating the first one though, we can exclusively focus on the second because after its result is known there is nothing left to compute. Ergo, the second sub-expression is in tail position.

Figure 76 displays the result of this analysis as a grammar of our model language with tail positions marked up.

AssExpr  =
  Int ||
  (node O AssExpr AssExpr) ||
  (if-0 AssExpr AssExprt AssExprt) ||
  Var ||
  (decl Var AssExpr AssExprt) ||
  (fun Var AssExpr) ||
  (call AssExpr AssExpr) ||
  (set  Var AssExpr) ||
  (sequ AssEexpr AssExprt)

Every one of these expression is in tail position if it is at the top level of a function body.

Figure 76: A Grammar with Asterisk Indicating Tail Position

The tail position must be inside those sub-expressions that are starred. Evaluating any other sub-expression demands that some other computation must be performed after the expression is done.

When a function call shows up in a tail position it is dubbed a tail call.

All calls of continuations must be tail calls in a gradually converted expressions. So, in the second Racket expression in figure 75 the call to k is a tail call; in the third one it is not. When halt-k simply returns its argument value, calling a continuation in tail position or not doesn’t matter; but when halt-k stops—say by raising an exception—it won’t accidentally ignore calls outside of tail positions. Figure 77 shows a correct conversion with a set-up you can do in your languages.

Lectures/20/cps-correct.rkt

  #lang racket
   
  (require "cps-theorem-imports.rkt")
   
  (define halt-k (λ (final-result) (raise final-result)))
   
  ;; - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
  ;; in our model language
   
  [call [fun f (node * (call f 10) (call f 20))]
        [fun x (node + x 42)]]
   
  ;; - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
  ;; in RACKET (or your favorite language) 
   
  (with-handlers ([number? values])
    ((λ (f) (* (f 10) (f 20)))
     (λ (x) (+ x 42))))
   
  ;; - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
  ;; equip first function with continuation for delivering result
   
  (with-handlers ([number? values])
    ((λ (f k) (k (* (f 10) (f 20))))
     (λ (x) (+ x 42))
     halt-k))
   
  ;; - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
  ;; equip second function for delivering a result, call it with halt-k
   
  (with-handlers ([number? values])
    ((λ (f k) (k (* (f 10 halt-k) (f 20 halt-k))))
     (λ (x k) (k (+ x 42)))
     halt-k))
   
  ;; - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
  ;; continuations constructed and called properly
   
  (with-handlers ([number? values])
    ((λ (f k) (f 20 (λ (of-20) (f 10 (λ (of-10) (k (* of-10 of-20)))))))
     (λ (x k) (k (+ x 42)))
     halt-k))
   

Figure 77: A Gradual CPS Conversion, Done Correctly

A second look shows that all function calls are in tail position. Now that we have successfully converted the expression in Racket we can port it back to our model language and the way our cps works:
[call
  [call [fun k
           [fun f
             [call
               [call f [fun of-20
                         [[call f [fun of-10
                                    [call k [node + of-10 of-20]]]
                                  10]]]
                       20]]]]
        [fun final final]]
  [fun x (node + x 42)]]
In our model language we have nested calls because functions can consume only one argument at a time. But, because the first call consumes the continuations must immediately return to consume the actual argument, each call has an extremely limited extent of a single computation step.

Finally, when you’re all done with the conversion, inspect your term to make sure

  1. no function ever returns to its caller directly; it always calls a continuation

  2. every function call is in a tail-position

Clause 2 works for your language because functions may consume several arguments at once.

    ← prev  up  next →