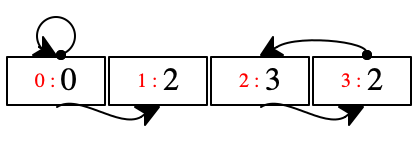24 --- Memory, Safety

7.7.0.3

24 — Memory, Safety

Friday, 03 April 2020

Presenters (1) Alexander Takayama & (2) Khalil Haji & Griffin Rademacher

Stop! Is the CESK interpretation of Expr sound? Can it produce nonsensical results? Can it get stuck in a state that isn’t final?

Soundness aka (Memory) Safety

As spelled out, the mathematical model could be interpreted either way. The transition table carefully spells out when a value is expected to be a plain value, when a location, or when it doesn’t matter.

If the set of Locs is disjoint from the set of Numbers (no common elements), then the machine gets stuck if locations are used as numbers or vice versa.

If the set of Locs is, say, the set of natural numbers, then the machine may conflate locations and numbers when transitioning from one state to another. The distinguishing new error state is one in which the machine attempts to retrieve a value from a location that does not exist. Other error states disappear, because multiplying locations, for example, is now perfectly fine. The trade-off is a horrible one as those of you had the pleasure of writing code in C. C++, or Objective C can witness.

Consider the evaluation of an expression that adds the result of an allocation to 3:

((1 alloc 2) + 3)

Or even worse, an expression that performs arithmetic on locations and then retrieves the value in the resulting store location:

[((1 alloc 2) + 1) dot left]

This kind of calculation with locations may even make some sense when the programming language spells out the layout of data structures in the store’s memory (say, the arrangement of array fields in sequential order with no padding for the coefficient for an access polynomial).

And to drive home the potential problems, here is an expression that runs just fine on our CESK machine, too:

([(1 alloc 2) * (3 alloc 4)] dot left)

It multiplies two locations—hey! they might just be numbers—and then retrieves the value at the resulting number. Whether this number is a valid location or not depends very much on many factors, including the arithmetic of * (small vs big nums), the size of the memory in the store, and so on.

So how does the machine behave on such expressions? Which behavior is better?

If locations are drawn from the set of numbers ... In papers on programming language research, you might see this idea expressed as follows:

Loc ⊆ Number

Let’s see how the above expressions evaluate if Loc is just the set of natural numbers. Here is the first one:

*C	*E	*S	*K
((1 alloc 2) + 3)	∅	∅
(1 alloc 2)	∅	∅	[L ∅ + 3]
0	∅	0 ↦ 1, 1 ↦ 2	[L ∅ + 3]	pop
0	∅	0 ↦ 1, 1 ↦ 2	[L ∅ + 3]
(0 + 3)	∅	0 ↦ 1, 1 ↦ 2
3	∅	0 ↦ 1, 1 ↦ 2		pop
3	∅	0 ↦ 1, 1 ↦ 2

A call to alloc places the two given values into two neighboring locations in the store—0 and 1 because the store is still empty—and returns the first one. Since the CESK machine does not distinguish locations from numbers, it adds this 0 to the 3 and the final state represents the result 3.

Is a location a result that a user expects?

The second expression exhibits the danger of seemingly legal calculations with addresses:

*C	*E	*S	*K
(((1 alloc 2) + 1) dot left)	∅	∅
((1 alloc 2) + 1)	∅	∅	[L ∅ dot left]
(1 alloc 2)	∅	∅	[L ∅ dot left], [L ∅ + 1]
0	∅	0 ↦ 1, 1 ↦ 2	[L ∅ dot left], [L ∅ + 1]	pop
0	∅	0 ↦ 1, 1 ↦ 2	[L ∅ dot left], [L ∅ + 1]
(0 + 1)	∅	0 ↦ 1, 1 ↦ 2	[L ∅ dot left]
1	∅	0 ↦ 1, 1 ↦ 2	[L ∅ dot left]	pop
1	∅	0 ↦ 1, 1 ↦ 2	[L ∅ dot left]
(1 dot left)	∅	0 ↦ 1, 1 ↦ 2
2	∅	0 ↦ 1, 1 ↦ 2		pop
2	∅	0 ↦ 1, 1 ↦ 2

The addition of 1 to the location happens to yield the location of the second value places in the store, and the CESK machine retrieves the 2 just fine.

What if we had added -1 to the result of alloc? What if we had added 3? Which value would we get?

The model presented here is precisely what languages such as C, C++, and Objective C implement. Many Python libraries are actually just thin veneers over such C code, which makes some of them blazingly fast—but also makes the language basically unsafe.

When locations are numbers, we speak of a language that lacks memory safety because it can access any location, whether it is meaningful or not.

Stop! Run the location-multiplication expression on your CESK machine? What does it yield?

If locations are distinguishable from numbers ... Now suppose Loc and the set values do not overlap:

Loc ∩ Number = ∅

Here we specifically imagine that Loc are bold-faced natural numbers, which are not the same as pale-faced ones. In this case the CESK machine can distinguish the two kind of values and, as specified, runs into a stuck state:

*C	*E	*S	*K
((1 alloc 2) + 3)	∅	∅
(1 alloc 2)	∅	∅	[L ∅ + 3]
0	∅	0 ↦ 1, 1 ↦ 2	[L ∅ + 3]	pop
0	∅	0 ↦ 1, 1 ↦ 2	[L ∅ + 3]
(0 + 3)	∅	0 ↦ 1, 1 ↦ 2

The tabular specification implies the existence of a FAILED state, so the machine transitions there and stops.

If a language handles Locs in this manner, it satisfies the property known as memory safety.

Tagged Integer In the world of real stores and even abstract machines, natural numbers do not come in bold face. In an implementation we tag the integer. At the hardware level this corresponds to reserving a bit (or more) per word whose setting tells the “reader” whether it is a location—called pointer at this level—or a number. Many implementations use several bits for tagging to distinguish several kinds of values (array values, locations, etc). In a software implementation, we may wrap natural numbers in structures, e.g., (location 2), to indicate that it is a “bold” or a “tagged integer.” In mathematical papers, such a tag or wrapper is left implicit except for papers that dig into the underlying set theory.

Note If you now revisit the Type Soundness theorem from 12 — The Truth, you see that the outcomes of evaluating programs in an untyped language with safe guards against meaningless access to the store are completely analogous to those of a typed language:

the program either returns a properly computed value
or it runs forever
or it stops with a well-known exception if the basic “arithmetic” calculations go wrong.

It is thus justified to speak of soundness in these cases, too.

There are more Control Codes than Expressions

The trace above reveals something else: locations can become a part of the control code.

First, this kind of property distinguishes the CESK machine from a virtual machine or a hardware machine.

Second, this property is somewhat of an artifact of executing instructions directly in the *C register instead of a dedicated, separate part of the machine.

Alternatively, this could be avoided with a separate set of “pop” instructions or with an arrangement where only variable definitions allocate storage and place the location into the environment.

Third, as a consequence, locations can show up only in the control code register as the immediate operands of a control code, so they are easy to find.

Memory Layout

All programs in our small language terminate, and we know exactly how many store locations it allocates: twice the number of alloc expressions. Nevertheless it can create rather complex memory configurations. With this language a program can directly reach and change every location. The even-numbered locations always represent the left part of a pair; the odd-numbered locations contain the right part.

The list of colors used is blue, orange, red, purple, pink. If you have difficulties reading these colored texts, please send email with concrete suggestions for an alternative color list. Consider this expression:

[decl 'z [decl 'y (1 alloc 2)1

(decl '_ (y set-left y)2

[decl 'x (3 alloc 4)3

(decl _ (x set-right x)4

(decl '_ (y set-right x)5

'x))])]

'[[[z dot right] dot right] dot right]]

The two alloc expressions clearly demand the use of four locations. The set-left and dot right expressions create whimsical connections among these locations. The (green) “pair arithmetic” chases from 'z (which is clearly 'x) “to the right” three times even though the x consists of only two values.

Here are the different stores that this program creates during its life time:

time	store at t
t = 1		allocate the pair [1,2]
t = 2		set the left part of the first pair to itself
t = 3		allocate a second pair, [3,4]
t = 4		set this second pair's right part to itself
t = 5		set the first pair's right part to the second pair

The small red numbers are the locations, the black numbers are the content. If the content is a location l, an arrow points from the center top of the box to the center top of l; if there is no arrow, the black number is an integer value. While the environment only ever contains even-numbered locations (why?), the arrows at the bottom of the store indicate that a program can reach every odd-numbered location from its neighbor to the left.

Let’s generalize from this example to insights about the store. What this example demonstrates is that the store evolves into a graph with all kinds of connections:

a location can point to itself; see location 0
an even-numbered location such as 0 implicitly points to its neighbor
two locations can point to the same one; see 2, reachable from 1 and 3
chasing arrows can directly and indirectly get us into a “loop;”
with 'z and 'x pointing to 2, you can now see why the three steps in the above program on a single pair succeed just fine;
see the chain of arrows starting at 0, which implicitly goes from there to 1, explicitly to 2, implicitly to 3, and explicitly back to 2
but, some locations are not reachable from the other registers of the machine;
see location 0, which is assigned to the variable 'y which gets eliminated from the environment (together with 'x) when the inner nests of decl return the value of 'x and assigns it to 'z

And this brings us to the next topic, managing memory.

Memory Management

When a programming language supplies a primitive such as 'alloc, developers are guaranteed to write code that sooner or later exhausts a computer’s memory capacity, because contrary to all rumors, even several gigabytes aren’t enough.

The language implementation combines the generated code with a runtime system; until now, we thought of this system as the prelude that defines all primitives. But there’s more to a runtime system, and this is the last major critical topic of this course.

How does your code get memory? It is the job of the operating system to manage scarce resources: network access, connections to a monitor, printing, time, and memory. With time, we mean CPU; there’s just a few but on the average a computer runs many more programs than that. So the OS allows every program to run every so often for a limited amount of time on (some of) the CPU(s).

Some people have predicted for a decade or two that the operating system will also provide a memory management service, like the one we’re discussing this week, to every running program. It hasn’t happened yet. What has happened is the emergence of two major runtime system as platforms: the JVM and the .NET system. All language implementations that target these platforms automatically benefit from the built-in garbage collector.

The operating system also reserves a certain amount of memory for every program. It is up to the program and the linked-in runtime system to manage this space.

So what does a runtime system do when your program has 'alloced all the space? When it has exhausted the store? It figures out what parts of the allocated memory are garbage.

The Truth GarbageT is any location that, when made inaccessible for the rest of a program evaluation, has no impact whatsoever on the visible behavior of the program.

As always, the truth isn’t decidable, which makes computer science and especially programming languages an interesting subject. Decidable means that there is no algorithm that consumes the state of a CESK machine and a location and produces a Boolean (with #true meaning the given location is garbageT and #false meaning it is not).

The Proof GarbageP is a location that, given the contents of the registers of a CESK machine, can be proven (by some algorithm) not to have any impact on the rest of the evaluation.

The Key GarbageP can be reclaimed and used again for other purposes.

The idea of garbage collection is due to the MIT Lisp team in the mid 1960s. Edwards implemented the first known garbage collector.

As with many ideas in programming languages, the history of garbage collection dates back many decades and, again, to the Lisp family of programming languages. Over this time researchers have expanded this idea to an area that is large enough to fill several courses. So here are some ideas you will encounter when people discuss garbage collection:

free ~~ Old programming languages, such as C, C++, Objective C and some more, provide a free function. A developer uses this function to tell the memory management system that a specific location is available for re-use. It is the responsibility of the developer to make sure that the program no longer needs access to the current value in this location. If the developer is wrong, we speak of a dangling pointer problem.
reference counting ~~ For the longest time, Python used a schema known as reference counting. Every location l comes with a “partner” location that contains the number of times l is referenced in the program. When this counter is 0, the memory management system may recycle the two locations.
Besides the cost and complexity of maintaining thus counter, it is also difficult to account for cycles in the memory graph. While some languages still use this old-fashioned scheme, most of those also support a garbage collection algorithm.
tracing garbage collection ~~ The most common algorithm in use starts from the (equivalent of the) E and K registers, follows the implicit and explicit arrows to all reachable locations, and recycles the others as garbage. We will study this algorithm in the next lecture.
conservative garbage collection ~~ Due to Boehm, a colleague of mine at Rice. The preceding description assumes that the algorithm can distinguish between integers (natural numbers) and locations and that it is possible to find all roots (source) locations in E and K. If the programming language design does not allow to make these distinctions, we speak of a non-cooperative I prefer “hostile” and told Boehm at the time. language. The idea of a conservative collector is to make, well, conservative guesses at what could be a location as opposed to a number and not recycle it. Furthermore, unlike tracing compilers which move “live” data from one place to another to reclaim garbageP memory, a conservative collector leaves it in place.
Note The word “conservative” is bogus but established terminology. Every garbage collector algorithm is conservative with respect to garbageT. And usually the word “conservative” is used when we speak of proof vs truth—for example when we discuss the foundations of type systems or static analysis algorithms in compilers. But alas, the word has taken hold.
If you are forced to program in C-like languages, consider the use of the Boehm conservative collector.
generational garbage collection ~~ Most people believe I use this word with its religious connotation only, not in the loose sense of “conjecture.” that allocated memory “dies young.” That is, locations that have been in use for a long time will remain in use, and recently allocated locations are more likely to be reclaimed.
Modern garbage collectors accommodate this idea with generations. They place survivors—locations in long time use—into one region of allocated memory and recently allocated locations in a nursery, and this nursery is inspected for garbage more frequently than the region for survivors. When a location has lived for a certain number of garbage collections in the nursery, it is moved to the “old people’s home.”
Clinger, a colleague who retired in 2019, conducted research in garbage collection. For the past decade or so of his active life, he tried to publish results that seriously question the “young locations die early” hypothesis. He has significant evidence that it applies only in some situations and that generational collectors may have fewer benefits than acclaimed.
concurrent garbage collection ~~ All of the above algorithms assume that, when your program runs out of memory and must allocate, we can stop the execution of the program (save all registers somewhere), inspect the store, collect the garbage, and re-start the program from where we stopped it. Hence they are called “stop the world” garbage collectors.
In some situations we may not wish to stop the program. This is mostly true for real-time system where a program must control physical objects (trains, planes, ships, missiles, medical instruments) the entire time.
To accommodate such situations, researchers develop targeted virtual machines with garbage collectors that run in parallel to the main program. These algorithms are extremely complex and costly. They are only now emerging for commercial use.
Prof. Vitek, while still at Purdue, worked on this problem with colleagues at IBM and eventually founded a small company to commercialize a concurrent garbage collector for a specialized Java Virtual Machine.
Crazy Ideas ~~ Remember that we discussed how to get back to the program from the state of the registers with the introduction of a new register. So, when we stop the program evaluation, we can actually re-construct a program that corresponds to the current state of the CESK machine—not the source program. Then we can apply a type inference algorithm to this reconstructed program. Every location—represented as a variable—whose type is inferred to be just a type variable is garbage.
Why?
A group at NYU and another one at INRIA France pursued this direction of research for a decade or so. In principle, this algorithm can discover more garbage than a tracing collector. But performing a type inference algorithm in the inner loop of a garbage collection world is costly. Nobody has so far succeeded in making it affordable.

But, remain aware, that you really know nothing about the field of garbage collection—other than that is truly complicated.

Which Programming Language is Better for the Developer

Managing locations and managing allocated memory is one of the most critical concerns in the design of programming language runtime systems.

Until the late 1990s, languages that allowed the conflation of numbers and locations dominated the software development landscape.

Until then, two claims dominated our world:

(1) people are better than “computers” (a language’s runtime system together with the hardware) at managing locations,

and anyways,

(2) this kind of store access is needed to make programs fast.

The first claim is complete bogus and we actually knew that. Given that a program manages dozens, hundreds, and thousands of allocated locations—possibly via equally many software developers—and given that we have used computers for accounting tasks for 60 years, we clearly have a contradiction on hand. People just refused to see it.

The second claim has some truth to it in extremely narrow niche application areas. It may also hold when you have a brand-new machine and no real language on it to develop any software with, though in the 1970s and 80s we had hardware that could have distinguished locations from numbers.

As I have mentioned before, IBM ran a large-scale productivity experiment comparing C++ with Java, and Java won big time. Initially people thought it was type soundness that made Java superior to C++, but soon they realized it was really memory safety that saved developers tons of development time.

Zorn, a researcher at Colorado around the same time, analyzed many realistic C/C++ programs, equipped them with a garbage collector, and ran timing comparisons. To his surprise, the variants with garbage collectors ran much faster than those with manually managed memory. He knew he wouldn’t be able to get this result published—given the dominant opinion among computer “scientists” at the time—and worked hard to eliminate inefficiencies from the programs to narrow the gap. Even then he had a hard time getting this result published.

Lesson Be skeptical of scientists and “consensus science.”

Alternative One can imagine a language that supports a separate domain of location numbers and arithmetic on such things. One can also imagine a language that allows programmers to state type-like claims about the ownership of locations so that two collaborating developers can get the “type checker” to validate their handling of locations.

This notion of ownership type was first conceived by Jan Vitek (a Northeastern professor now), was further developed by Jesse Tov (a Northeastern PhD who left when Vitek arrived), and became the foundation of the Rust programming language.

← prev up next →

	Abstract
	General
	Lectures
	Readings
	Email, Office Hours, Etc.
	Lab Book
	In-Class Reviews
	Delivery
	Assignments

	1 — Programming Languages: Research and Teaching
	2 — Parsing
	3 — Scope, Compilation
	4 — Compilers; Fun
	5 — Help!
	6 — Recursive Functions
	7 — Errors and Ordering
	8 — Assignments
	9 — Store Passing
	10 — What and When
	11 — Types & Proofs
	12 — The Truth
	13 — Poly Types
	14 — More Types
	15 — JULIA Types
	16 — Gradual Types
	17 — CPS
	18 — ONLINE
	19 — CANCELLED
	20 — Control from CPS
	21 — State Machines
	22 — C, CC, CK
	23 — CEK, CESK
	24 — Memory, Safety
	25 — Space
	26 — Q & A
	27 — Expressiveness
	28 — Monads
	29 — Continuations