►Principles of Programming Languages
▼Lectures
•26 — Q & A
7.7.0.3
    ← prev  up  next → 

26 — Q & A

Friday, 10 April 2020

What Are Macros

Short Macros are functions that the parser runs on portions of the input.

Long Here is the (essence of my) parser for Toy from 9 — CPS:
; [JSexpr -> AST]
; JSexpr is Racket's internal representation of JSON,
; AST is my Racket-data representation of valid JSON programs
(define (parse stx)
  (match j
    [(? json-string-not-keyword? x)
     (parse-variable x)]
    [(? integer?)
     (parse-integer stx)]
    [`[["let" ,(? json-string-not-keyword? x) "=" ,rhs] ... ,body]
     (unless (generic-set? x) (error 'parse ERR-SET "definition" x))
     (ast-block (map parse-decl x rhs) (parse body))]
    [`["fun*" ,(and parameters `(,(? json-string-not-keyword?) ...))  ,body]
     (unless (generic-set? parameters) (error 'parse ERR-SET "parameter" parameters))
     (ast-fun* (map parse-variable parameters) (parse body))]
    [`["call" ,fun ,arg ...]
     (ast-call (parse fun) (map parse arg))]
    [`["if-0" ,tst ,thn ,els]
     (ast-if-0 (parse tst) (parse thn) (parse els))]
    [`["stop" ,body]
     (ast-stop (parse body))]
    [`["grab" ,(? json-string-not-keyword? x) ,body]
     (ast-grab (parse-variable x) (parse body))]
    [_ (error 'parse "bad expression ~e" stx)]))
The highlights show where direct property checking happens and parse errors are signaled.

The addition of macros demands two changes to this setup. First, the parser must recognize macros and deal with them differently. Second, the language must provide a mechanism for registering functions as macros.

Let’s discuss the second change first. The most common way to coordinate macros with the parser is to set up a table that maps names to functions defined at parse time:
(define macro-table
 (dictionary
   "seq*" (lambda (stx)
             (match stx
               [`["seq*" ,first ,others ...]
                `["call"  ,(make-begin-function (+ (length others)  1))
                         ,first ,@others]]
               [_ (error 'seq* "bad syntax")]))
   ...   ...))
 
; [JSexpr -> JSexpr]
(define-at-parse-time (make-begin-function n)
   (define xs (build-list n gensym))
   `["fun*" ,xs ,(last xs)])
We also want macro-table to be extensible; see below.

The keys in this extensible macro-table are additional keywords that the parser must recognize. The values are macro transformers.

(define (parse stx)
  (match stx
    [(? json-string-not-keyword? x)
     (parse-variable x)]
    [(? integer?)
     (parse-integer stx)]
    [`[["let" ,(? json-string-not-keyword? x) "=" ,rhs] ... ,body]
     (unless (generic-set? x) (error 'parse SET "definition" x))
     (ast-block (map parse-decl x rhs) (parse body))]
    [`["fun*" ,(and paras `(,(? json-string-not-keyword?) ...))  ,body]
     (unless (generic-set? paras) (error 'parse SET "parameter" paras))
     (ast-fun* (map parse-variable paras) (parse body))]
    [`["call" ,fun ,arg ...]
     (ast-call (parse fun) (map parse arg))]
    [`["if-0" ,tst ,thn ,els]
     (ast-if-0 (parse tst) (parse thn) (parse els))]
    [`["stop" ,body]
     (ast-stop (parse body))]
    [`["grab" ,(? json-string-not-keyword? x) ,body]
     (ast-grab (parse-variable x) (parse body))]
    [`[,(? (λ (x) (dictionary-has-key? macro-table x)) keyword) ,x ...]
     (define macro-transformer (dictionary-ref macro-table keyword))
     (parse (macro-transformer stx))]
    [_ (error 'parse "bad expression ~e" stx)]))

Figure 100: A Rudimentary Macro Parser

Now the change to the parser is almost obvious; see figure 100. The added clause recognizes that a macro transformer is defined in macro-table. In response, parse retrieves this transformer function, hands over the current JSExpr tree, and parses the result of the transformation.

Most modern compilers use such a macro system to translate the surface syntax into a small subset, which is then translated to assembly.

Lisp was the first programming language with such a macro system, dating back to the middle of the 1960s. All of its successors—Clojure, Racket, Scheme—have sophisticated variatnts. Recently conventional languages—JavaScript (sweet.js), Rust, Scala—have started catching up.

Some Macro Problems Say we wish to add a macro that is like "if-0" but checks whether the test expression evaluates to some number n not 0. The syntax design is easy:

["if-0", n, tst, thn, els]

This variant of our conditional has one more sub-expression—the first—and it is the number we wish to compare to the value of tst. And this statement informally explains the meaning of this new language construct.

So here is a first design of the macro, literally translating the idea into code:

    ...

    "if-n" (lambda (stx)

             (match stx

               [`["if-n" ,n ,tst ,thn ,els]

               `[,"if-0" ["call" "+" ["call" "*" -1 ,n] ,tst]

                        ,thn

                        ,els]]))

    ...

Stop! Spot the problem with this first design.

The problem is that tst may evaluate to a closure, and this value should count as “not 0” but the addition expression signals an error instead.

Toy cannot express a “is this a number” test, but let’s imagine it for a moment. Then we could first check whether tst evaluates to a number and, if so, compare it to n:

    ...

    "if-n" (lambda (stx)

             (match stx

               [`["if-n" ,n ,tst ,thn ,els]

               `["if-0" ["call" "number_p" "tst"]

                        ["if-0" ["call" "+" ["call" "*" -1 ,n] "tst"]

                                ,thn

                                ,els]

                       ,els]]]))

    ...

Stop! Spot the problem with this second design.

The problem is that this macro evaluates tst twice. If tst performs an assignment, this effect happens twice—which is clearly undesirable.

So, we declare a local, temporary value and first check its nature as a number and then compare it to 0:

    ...

    "if-n" (lambda (stx)

             (match stx

               [`["if-n" ,n ,tst ,thn ,els]

               `[["let" "not_tst" "=" ,tst]

                  ["if-0" ["call" "number_p" "not_tst"]

                          ["if-0" ["call" "+" ["call" "*" -1 ,n] "not_tst"]

                                  ,thn

                                  ,els]

                          ,els]]]))

    ...

Stop! Spot the problem with this third design.

The idea of hygienic expansion is due to Kohlbecker, Friedman, yours truly, and Duba. The problem with this design is that the declaration of "not-tst" binds all references to this variable, including those in thn and els. Again this is undesirable and known as the hygiene problem and properly solved by a hygienic macro expansion process, far more sophisticated than the one outlined above.

True Power The above sketch of a “macro system” defines macro transformers in the implementation language, not the implemented language. This means that the author of the model, the interpreter, or the compiler may write macro transformers but the Toy programmer cannot.

The principle of some languages—including Racket—is roughly

software developers are first-class citizens,

meaning these languages empower ordinary developers to create macros in the implemented language itself.

To this end, the implemented language itself must come with

  1. data structures that can (conveniently) data-represent the “read” information,

  2. a mechanism for extending the macro table, and

  3. a facilities for easily manipulating—destructuring and creating—this syntactic data so that it becomes easy to write functions such as the one for "seq*" in the implemented language..

In terms of Toy, these bullets mean the language must have a data representation, including a powerful API, for what the JSON reader delivers. Because JSON is so close to the one of JavaScript’s core data structures, it is not surprising that the idea of language processing (transpiling) has taken a hold there, giving rise to TypedScript for example.

This may also explain why the Lisp world got to macros so early. Its core data structure and the data representation of what the reader produces coincide. While this is not quite the case for Racket—the reader delivers S-expressions enriched with many attributes useful for error reporting and debugging—the language still provides a rich way of representing syntax as structures and using one of the richest pattern-matching sub-language for working on it. Here is the example from above.

Lectures/26/seq.rkt

  #lang racket
   
  (begin-for-syntax
    (require syntax/parse (only-in racket last))
    
    #; {[Listof Syntax] -> Syntax}
    (define (make-begin-function lo-stx)
      (define xs (generate-temporaries lo-stx))
      #`[lambda #,xs #,(last xs)]))
   
  (define-syntax
    seq*
    (lambda (stx)
      (syntax-parse stx
        [(seq* first others ...)
         #`(#,(make-begin-function #'(first others ...))
            first others ...)])))
   

Figure 101: (elem The (tt seq*) Macro in Racket)

Racket permits a much more precise expression of this idea. This definition is deliberately expressed in the exact same manner as the above “Toy macro” to drive home the three bullets: syntax structures can be deconstructed via pattern-matching, can be created from templates, and transformers are really just functions that exist at the “syntax” phase—that is, the time when parse is active—of processing a program. The last line extends the macro table with this transformer function for the token seq*.

This brings us to structures and pattern matching.

Records, Structures

Fundamentals I introduces structures to data-represent related pieces of information. A structure definition in the teaching languages of this course has the following shape:

(define-structure name [field1 ... fieldn])

The informal explanation in Part I of the http://www.htdp.org/2019-02-24/ says that each such structure definition defines n + 2 functions: one constructor, one predicate, and n selectors.

In Intermezzo 1 (Structure Type Definitions) this informal explanation is reformulated as a transpilation into n + 2 explicit function definitions:
(define tag-for-name (make-unique-name))
(define (make-name field1 ... fieldn) (list tag-for-name field1 ... fieldn))
(define (name? x) (and (cons? x) (equal? (first x) tag-for-name)))
...
(define (name-fieldi x)
  (if (name? x)
      (list-ref x italic{i})
      (error 'name-fieldi "expects a ~a, given ~e" name x)))
...
What this explanation hides is that tag-for-name may not be visible outside of this block of code. That is, we need a slightly different notion of scope than we have modeled so far.

Stop! This is a completely general explanation of structures. Instantiate this general explanation with a concrete number n and concrete identifiers for name, field1, ... fieldn.

You can think of this explanation as a sophisticated macro.

Or, you can build it into your Toy interpreter enriched with the pairs from lecture. Here are the pieces you have and how you can use them:

  • it is straightforward to create lists of arbitrary length from pairs

  • defining list-access functions is then an exercise

  • error is just a variant of the stop construct

  • function definitions and applications are already available as are conditionals

  • make-unique-name is the only “hard” issue left. It turns out that merely allocating a location from the store creates a unique token, and that token can be used as a tag.

Your work with While gives you an even better understanding of the store and how to allocate blocks of memory to deal with structures instead of arrays. Indeed, the lectures on mutable pairs and your homework on While also tell you how to inject assignment statements that deal with structures.

Objects, Dispatch

Objects resemble structures, and indeed, in some languages (Racket for example), we can use structures to implement an object. Classes are object factories.

  ;; a point in the 2-dimensional plain

  class Point {

    private x = 0

    private y = 0

  

    Point(x, y) {

      self.x = x,

      self.y = y}

  

    ;; compute the distance of this point to (0,0)

    public distance-to-origin() {

      return .. x^2 .. y^2 ..

    }

  

    ;; EFFECT change the coordinates of this point by the given deltas

    ;; then compute the distance to the origin

    public translate(delta-x, delta-y) {

      x = x + delta-x, y = y + delta-y,

      self.distance-to-origin() }

  }

  

  p = new Point(3,4)

  p.distance-to-origin-method()

  p.translate-method(9,1)

Figure 102: Classes and Objects, Pseudocode

Consider the pseudocode in figure 102. It defines a class, creates an instance, and performs two method calls. Every point object has two fields, one constructor, and two publicly visible methods.

It turns out that we can explain classes, objects, and object dispatch with what we have seen in this course: one-field/two-method cells; arrays (vectors); scope; and functions.

Take a close look at figure 103. Even though the code is written in Racket, the syntax resembles much more a cross between the language constructs of Toy (let, fun*, etc) and While (vec, let, etc). It is well within your abilities to modify either one of these two model languages to add the basic constructs.

Lectures/26/classes-and-objects.rkt

  #lang racket
   
  (require "../../Code/10/Other/rename.rkt")
   
  [let point-class =
    [seq* 
     [let distance-to-origin =
       (fun* (self instance)
             (fun* ()
                   (call sqrt
                         (+ (* [instance X] [instance X])
                            (* [instance Y] [instance Y])))))]
     [let DISTANCE = 0]
   
     [let translate =
       (fun* (self instance)
             (fun* (delta-x delta-y)
                   ([instance X] = (call + [instance X] delta-x))
                   ([instance Y] = (call + [instance Y] delta-y))
                   (call (call self instance DISTANCE))))]
     [let TRANSLATE = 1]
   
     ;; - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
     [let X = 0]
     [let Y = 1]
     [vec vtable = [distance-to-origin translate]]
          
     [let dispatcher =
       (fun* (instance method)
             (if (and (integer? method)
                      (<= 0 method (- (vector-length vtable) 1)))
                 (call [vtable method] dispatcher instance)
                 (error 'point-class "no such method ~e" method)))]
     (fun* (x-field0 y-field0)
           (seq*
            [vec instance = [x-field0 y-field0]]
            [fun* [method] [call dispatcher instance method]]))]]
   
  [let distance-to-origin = 0] 
  [let translate          = 1]
   
  ;; - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 
  [let p = (point-class 3 4)]
  (call (call p distance-to-origin)) ;; --> 5
  (call (call p translate) 9 1)      ;; --> 13
   
  [let q = (point-class 1 1)]
  (call (call q distance-to-origin))
  (call (call q translate) 2 3)
   
  ;; target.method(arg ...)
   
  ;; [if random(10) % 2 ==== 0
  ;;     p
  ;;     q].distance-to-origin()
  (call (call (if (even? (random 10)) p q) distance-to-origin))
   
   
   
   
   
   

Figure 103: Classes and Objects

The figure explains how to understand a class and its manufactured objects as functions:

  • The class is a function that constructs instances.

  • The scope of the class sets up the “transpiled” methods and puts them in a vector

  • Each instance is a function that consumes a method to which it should jump.

  • A method call uses the known vector index to extract the method and call the underlying function. This call supplies both vtable for self-calls and the field values of the current instance.

Stop! Why do you think the methods are collected in a table? Why are calls directed thru the table?

Imagine an extension of this class. It may add methods, inherit some, and override others. The vtable of this derived class will store the inherited methods and the overridden methods in the same slot as the base class. Thus, when a method in the derived class calls a method from the base class, which then calls an overridden method, the indirection through vtable ensures that each call gets directed to the proper target. In short, it is the representation of a class’s methods via a table that the fundamental template-hook pattern (see Fundamentals II) is realized.

Pattern Matching

Throughout the semester my code has employed a language feature called match. In principle, match is just a rather fancy conditional. Like cond from Fundamentals I, match sequentially searches the clauses and attempts to fit the given piece of data to the pattern part of the clause, which roughly corresponds to the conditional part of a cond. When it finds a fitting pattern, match evaluates the right-hand side—the answer part of a cond clause—and the value of this right-hand side becomes the value of the entire match expression.

From this perspective, the only interesting aspect concerns “fit” though because of this concern, there’s a bit more to “evaluate the right-hand side” than meets the eye. So, consider the following example, an excerpt from the code above:
(match j
  ...
  [`["call" ,fun ,arg ...]
   (ast-call (parse fun) (map parse arg))]
  ...)
Here match fits j against several patterns, among others against the call syntax. First we need to unroll the backquote and comma syntax:
(match j
  ...
  [[list "call" fun arg ...]
   (ast-call (parse fun) (map parse arg))]
  ...)
At this point, you can begin to see what “fit” might mean:

  • j must be a list

  • it must start with the string "call"

  • it may have to contain additional pieces.

But what are fun and arg here? What do the dots means?

In the context of a match pattern, variables such as fun and arg are declarations. They come without initial values because it is the fitting process that supplies these values. The presence of fun means that j must contain another element beyond "call". The presence of arg would mean that there must be a third one, except that arg ... really means any sequence of zero or more list elements works. Thus, if j is any of the lists below the datum fits the pattern:
; – 1
[list "call" "f" 1]
; fits if fun ~~ "f", arg ~~ [list 1]
 
; – 2
[list "call" "f" 1 [call "g" 2 3] 4]
; fits if fun ~~ "f", arg ~~ [list 1 [call "g" 2 3] 4]
 
; – 3
[list "call" [call "h" 1] 2]
; fits if fun ~ [call "h" 1], arg ~~ [list 2]

Once match determines that there is a fit, it uses the variables in the pattern to set up variable declarations for the right-hand side. For the above three examples, match creates the following local definitions:
; – 1
(local ((define fun "f")
        (define arg [list 1]))
 (ast-call (parse fun) (map parse arg)))
 
; – 2
(local ((define fun "f")
        (define arg [list 1 [call "g" 2 3] 4]))
 (ast-call (parse fun) (map parse arg)))
 
; – 3
(local ((define fun '[call "h" 1])
        (define arg [list 2]))
 (ast-call (parse fun) (map parse arg)))

In general, match is a macro that translates into a combination of cond and local. The fitting process is a process that traverses a pattern and a piece of data in parallel as long as their is a fit. All literal constants have to be equal. A variable in the pattern is made to stand for the corresponding piece of the given data. If there is a mismatch between two literal constants or the demanded shape (a list of two elements vs a list of three elements), the fitting fails and match moves to the next clause.

Different functional programming languages support different forms of pattern matching. Specifically, they differ in the notation of patterns that developers may write down. Racket’s is extremely rich allowing, for example, the dots notation to fit a variable to an entire sequence of data.

Pattern matching also serves different purposes. In an untyped language such as Clojure or Racket, pattern matching is merely a convenient way to deconstruct lists, trees, dictionaries, and even graphs. In a typed language with Hindley-Milner style inference (see 14 — More Types), pattern matching is essential for the type inference process. The pattern variables permit the type inference process to set up distinct type equations for distinct clauses and thus refine types to the needs of each clause.

Lexing, Parsing

To start with, these ideas are not programming language concepts as the research area understands itself in 2020 or how it understood itself in 2000 or even in 1980.

Ten years before, Chomsky has developed grammars and a hierarchy of languages, which it turned out matched what computer scientists came up with.

In the late 1950s, people began to understand that, like a natural language, a programming language comes with a vocabulary and a grammar. They then borrowed ideas from linguists to write down descriptions of all tokens in a language and all grammatically correct phrases. Software developers uses these descriptions as guides to coding up lexers and parsers. By the late 1960s, developers figured out that the process of going from such descriptions to the implementation made up a common pattern—and like all good developers abstracted over this pattern. Technically speaking, they created software that translated grammars for tokens and grammatical rules into lexers and parsers. Since then, only students in compiler classes or theory courses have written lexers or parsers by hand. Or students in Fundamentals I (see Finite State Worlds, Domain-Specific Languages, and A Glimpse at Parsing).

Sadly, developers also write half-baked parsers when they create batch programs. Such programs read raw text information from file, create internal data representations, and render the result as textual information again. Developers would in many cases be better off if they deployed the generators that create lexers and parsers via tools.

The College’s compiler course discusses this topic in much more detail.

Compilers

1 — Programming Languages: Research and Teaching defines compilers like this:

A-Interpreter = B-Interpreter o A-to-B-compiler

2 — Parsing adds that the creation of compilers is concerned with two sets of algorithms:

  • The primary goal is to make the generated code (in language B) use as little time, as little space, and as little energy as the compiler writer can imagine.

  • The secondary goal is to ensure that the compiler creates the code in O(n) time and O(n2) space. This was true for a long time, and compiler writes still strive for that. Except that they accept a second-degree polynomial for running time and even a third-degree one for space. The rare compiler writer goes way beyond second and third degree.

In this course we have seen three exemplary pieces of compilers:

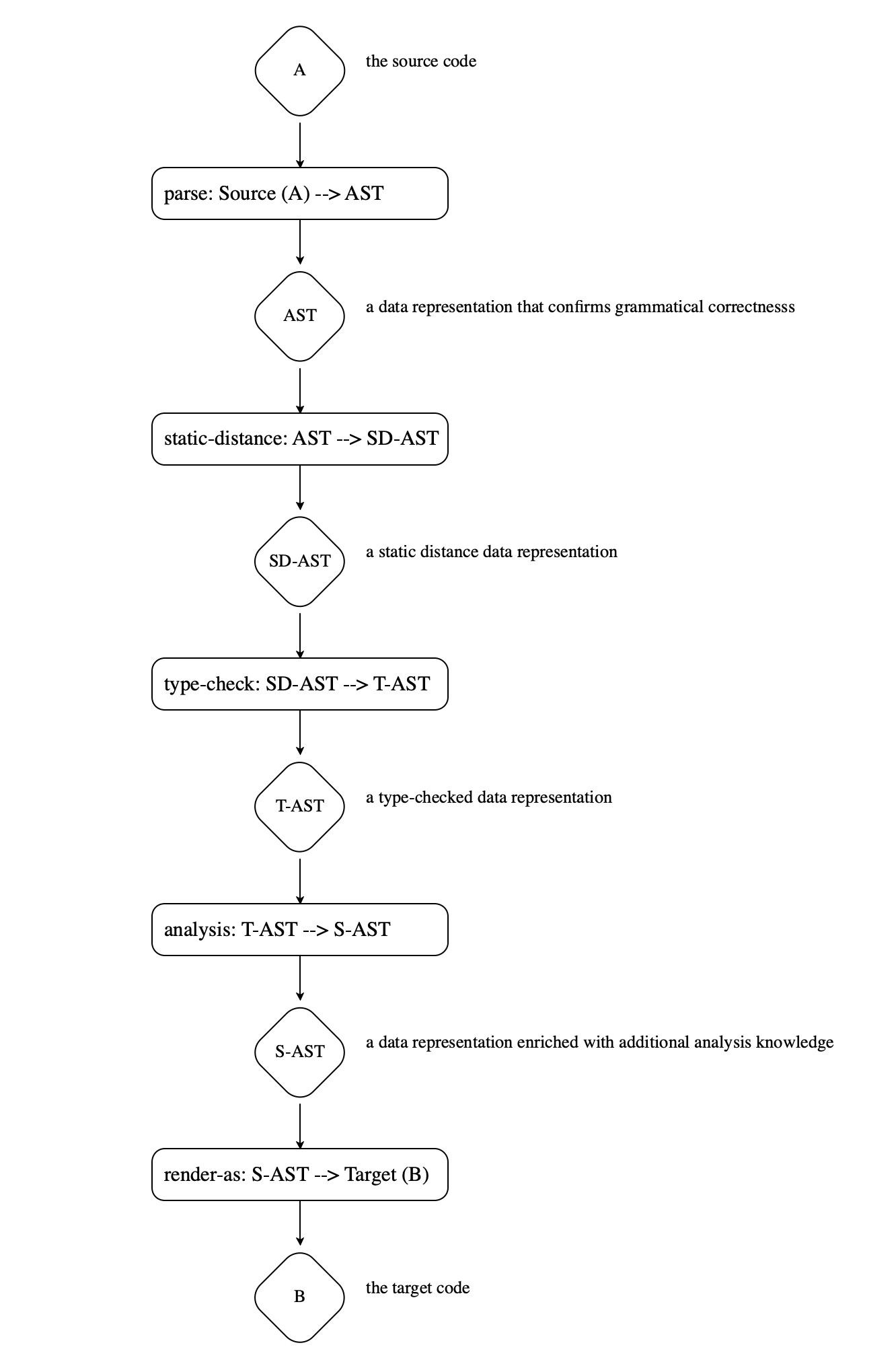
  • A parser generate an internal data representation for grammatically correct programs. It is appropriate to consider the AST a program in a different language, albeit a language that is somewhat close to the source language.

  • A static-distance translator replaces variable names with distance vectors. This process once again outputs a program in a different language.

  • A type checker ensures that the types part of the program represent true claims about the rest of the program. While our type checker simply signals an error when it finds a false claim, modern type checkers translate the typed program into a form that confirms the claims that reside in types. Again, this is a third translator.

So, here is another equation concerning the relationship between an interpreter and a compiler:

    A-Interpreter = B-Interpreter o

                           TypedIl–to-B-compiler o

                           AST-to-TypedIl-type-checker o

                           AST-to-SD-static-distancer o

                           A-to-AST-parser

Figure 104 presents the equation as a diagram, with explanations attached to each intermediate data representation.

image

Figure 104: The Classical Compiler Architecture

Each rounded rectangle represents one piece of the compiler—a pass—and each diamond is the program represented in a different language. People refer to the latter as intermediate representations or languages.

The most significant parts of a compiler is to find a smooth transition between the source tree (AST) and the expected final target language on one hand, and to find out as much as possible—claims!—about the program itself. Besides the type checker, the compiler proper may perform additional static checks. These checks may yield claims about the program that the types cannot express. For example, such a static checker might confirm that every indexing operation for arrays is within bounds. Hence the compiler would not need to insert run-time checks to guarantee the safety of the indexing operation. Over the past six decades, compiler writes have come up with many ways of checking and transforming the program to improve the performance of the generated code. The last step of the compiler is like your transpiler: it is like a toString method that renders the next-to-last intermediate program in the desired target language, B, so that the interpreter for B can run the code.

So:

A compiler-focused course on compilers is basically an algorithms course for a specific application domain.

A concept-oriented course on programming languages is about the ideas that sit atop lexing and parsing, namely, how to understand the meaning of programs and what enriches a programming language’s capabilities to express meaning.

    ← prev  up  next →